The objective of supervised learning is to find a hypothesis function $h$ that closely approximates the true function $f$, which underlies the data. Three primary components of a supervised learning problem can be considered¹: model representation, model evaluation and search method. Once the model representation and the model evaluation criteria have been selected, then the knowledge discovery endeavour is reduced to an optimization task of finding the parameters that define the hypothesis, which best fits the data. Both the model parameters and the hyper-parameters are considered².

Role of hyperparameter search in model training

An induction algorithm typically selects the best-fitting hypothesis by selecting optimal model parameter values from the hypothesis space using either closed-form solutions or some sort of induction algorithm. Hyper-parameters on the other hand determine the hypothesis space in which the induction algorithm operates (model complexity parameters), as well as fine-tunes the induction algorithm used to search the hypothesis space (algorithmic parameters).

For example, consider inducing an MLP neural network classifier by applying the back propagation algorithm. Hyper-parameter optimization will involve choosing the number of input features and the number of hidden layer nodes. Furthermore, the learning rate and strength of weight regularization used in the back propagation algorithm can also be selected. Given a hyper-parameter configuration, model parameter search involves finding the optimal hypothesis $h$ in the hypothesis space defined by the hyper-parameter configuration selected.

The problem of identifying a good hyper-parameter configuration $\vec{\lambda}$ from the set of all possible hyper-parameter configurations $\Lambda$ is called hyper-parameter optimization or model selection³. Hyper-parameter optimization can be summarized as,

where $\vec{\lambda}^{(1)},\dots,\vec{\lambda}^{(p)}$ are the $p$ hyper-parameter configurations evaluated and $R_{emp}(h^{\vec{\vec{\lambda}}})$ is the empirical loss² estimated for an induced model $h$ with hyper-parameter configuration $\vec{\lambda}$.

In most cases it is not computationally possible to evaluate each hyper-parameter configuration $\vec{\lambda} \in \Lambda$, therefore the set of hyper-parameter configurations $\vec{\lambda}^{(1)},\dots,\vec{\lambda}^{(p)}$ to evaluate has to be chosen.

Approaches to hyper-parameter search

Three basic approaches exist to select the hyper-parameter configurations considered: manual search, grid search and random search³:

1. In a manual search each hyper-parameter configuration $\vec{\lambda}$ is chosen by the modeller. Manual search is often used to provide insight into how learning algorithms respond to changes in hyper-parameter values. For expert users this is a useful technique to identify regions of interest in the hyper-parameter configuration space. However due to the subjective nature of manual search it is not easily reproducible, automatable or justifiable.

2. A grid search requires the preselection of a set of possible values for each of the $Q$ hyper-parameters in the hyper-parameter vector $\vec{\lambda}^{(Q\times1)}$. The grid search is performed by inducing hypotheses for each possible combination of hyper-parameter values. The number of configurations tested in a grid search is $\prod_{q=1}^Q L_q$ where $L_q$ is the number of values selected for hyper-parameter $q$. Though grid search is reliable in low dimensional spaces, it becomes prohibitively computationally expensive in higher dimensional spaces (larger values of $Q$) and at finer hyper-parameter value resolutions (large values of $L_q$). Furthermore, selecting a manageable and appropriate resolution for each hyper-parameter is problematic and extending the grid requires commitment to a much larger experiment.

3. Within a random search, hypotheses are induced independently, each model using a hyper-parameter configuration selected randomly from the predefined range of allowable hyper-parameter values. argue that a random search can find hyper-parameter configurations that are at least as good as those found in traditional grid search approaches, within a small fraction of the computational time. This is because the empirical loss estimated for a hypothesis may be highly sensitive to changes in some hyper-parameters and only weakly sensitive to changes in other hyper-parameters. A random search will explores more distinct values of the important hyper-parameter, and therefore more distinct empirical loss estimates (points on the empirical loss surface).

For example, consider the two-dimensional hyper-parameter spaces shown in the figure below. Assume the empirical loss estimated for a model is highly sensitive to changes in hyper-parameter one and only weakly sensitive to changes in hyper-parameter two. A grid search will waste trials by searching across parameter two, poorly covering the empirical loss surface while a random search will cover more points on the empirical loss surface by considering more values for both the important parameter and the unimportant parameter.

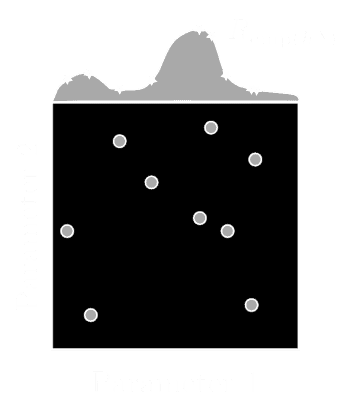
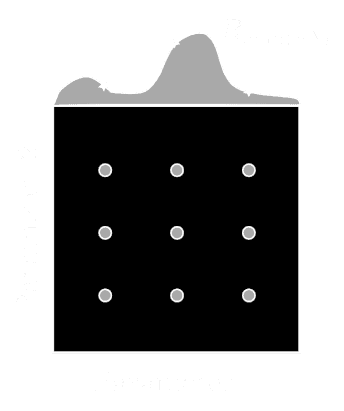
A random search also has the advantage that a search can be stopped and restarted at any time; searches can be carried out asynchronously; and because trials are independent new trials can be added and failed trials can be restarted as needed.

Notes

• Originally published as part of Wilgenbus, E.F., 2013. The file fragment classification problem: a combined neural network and linearprogramming discriminant model approach. Masters thesis, North West University.

References

Related tags

emerging technologydecision and data science